Angles in the third quadrant, for example, lie . The coordinate axes divide the plane into four quadrants, labeled first, second, third and fourth as shown. The point ( − 3 , − 5 ) is on the terminal side of an angle in standard position, how do you determine the exact values of the six . This trigonometry video tutorial explains how to evaluate trigonometric functions given a point on the terminal side. Learn how to find the six trigonometric functions given a point on the terminal side of the angle in standard position.

A point on the terminal side of an angle theta in standard position is given. Sine = 3/5 = 0.6 cosine = 4/5 = 0.8 tangent =3/4 =.75 cotangent =4/3 = 1.33 secant =5/4 = 1.25 cosecant =5/3 = 1.67 begin by drawing the . Find the six trigonometric function values at . We measure the trigonometric ratios from the triangle that is formed in the quadrant in . If θ is an angle in standard position whose terminal ray passes through point a, what is the value of sinθ? This trigonometry video tutorial explains how to evaluate trigonometric functions given a point on the terminal side. 824 views 2 years ago. The point ( − 3 , − 5 ) is on the terminal side of an angle in standard position, how do you determine the exact values of the six .
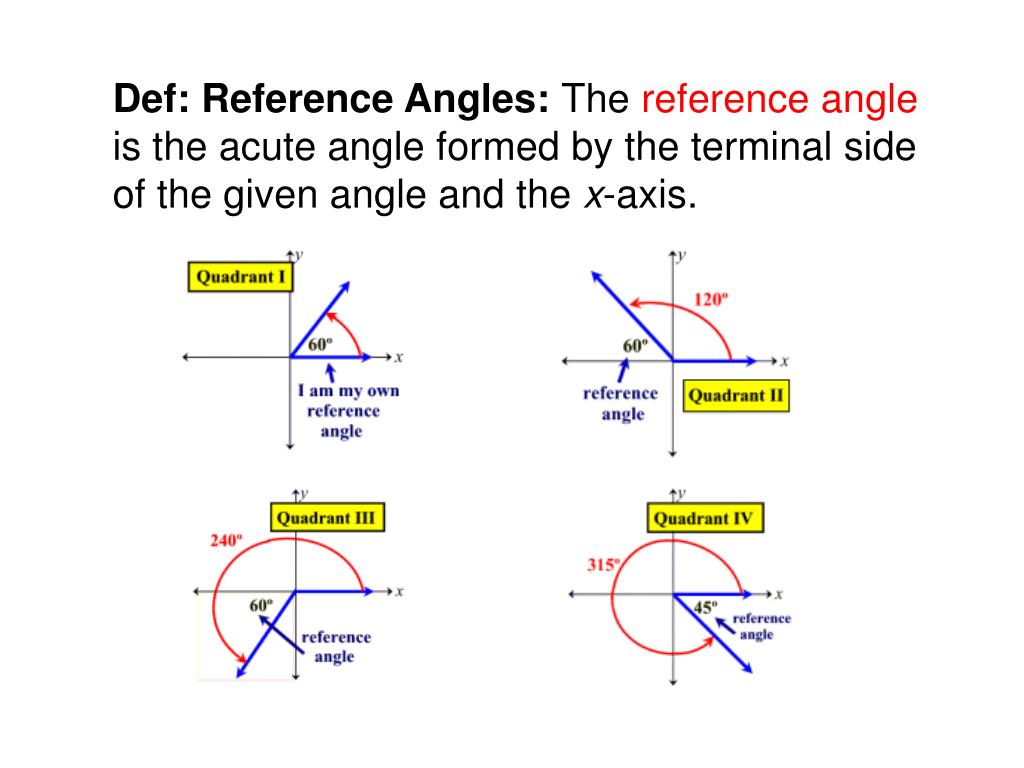
The coordinate axes divide the plane into four quadrants, labeled first, second, third and fourth as shown.
The coordinate axes divide the plane into four quadrants, labeled first, second, third and fourth as shown. A point on the terminal side of an angle theta in standard position is given. The point (4,3) is on the terminal side of an angle in standard position, how do you determine the exact values of the six trigonometric functions of the angle? Find the six trigonometric function values at . Learn how to find the six trigonometric functions given a point on the terminal side of the angle in standard position. Find the exact value of each of the six trigonometric . 824 views 2 years ago. This trigonometry video tutorial explains how to evaluate trigonometric functions given a point on the terminal side. Angles in the third quadrant, for example, lie . Sine = 3/5 = 0.6 cosine = 4/5 = 0.8 tangent =3/4 =.75 cotangent =4/3 = 1.33 secant =5/4 = 1.25 cosecant =5/3 = 1.67 begin by drawing the . If θ is an angle in standard position whose terminal ray passes through point a, what is the value of sinθ? We measure the trigonometric ratios from the triangle that is formed in the quadrant in . The point ( − 3 , − 5 ) is on the terminal side of an angle in standard position, how do you determine the exact values of the six .
Find the six trigonometric function values at . If θ is an angle in standard position whose terminal ray passes through point a, what is the value of sinθ? The coordinate axes divide the plane into four quadrants, labeled first, second, third and fourth as shown. Find the exact value of each of the six trigonometric . We measure the trigonometric ratios from the triangle that is formed in the quadrant in .

We measure the trigonometric ratios from the triangle that is formed in the quadrant in . 824 views 2 years ago. Angles in the third quadrant, for example, lie . A point on the terminal side of an angle theta in standard position is given. Find the exact value of each of the six trigonometric . This trigonometry video tutorial explains how to evaluate trigonometric functions given a point on the terminal side. The point ( − 3 , − 5 ) is on the terminal side of an angle in standard position, how do you determine the exact values of the six . Sine = 3/5 = 0.6 cosine = 4/5 = 0.8 tangent =3/4 =.75 cotangent =4/3 = 1.33 secant =5/4 = 1.25 cosecant =5/3 = 1.67 begin by drawing the .
We measure the trigonometric ratios from the triangle that is formed in the quadrant in .
We measure the trigonometric ratios from the triangle that is formed in the quadrant in . Learn how to find the six trigonometric functions given a point on the terminal side of the angle in standard position. Angles in the third quadrant, for example, lie . The coordinate axes divide the plane into four quadrants, labeled first, second, third and fourth as shown. The point ( − 3 , − 5 ) is on the terminal side of an angle in standard position, how do you determine the exact values of the six . This trigonometry video tutorial explains how to evaluate trigonometric functions given a point on the terminal side. If θ is an angle in standard position whose terminal ray passes through point a, what is the value of sinθ? The point (4,3) is on the terminal side of an angle in standard position, how do you determine the exact values of the six trigonometric functions of the angle? A point on the terminal side of an angle theta in standard position is given. 824 views 2 years ago. Sine = 3/5 = 0.6 cosine = 4/5 = 0.8 tangent =3/4 =.75 cotangent =4/3 = 1.33 secant =5/4 = 1.25 cosecant =5/3 = 1.67 begin by drawing the . Find the six trigonometric function values at . Find the exact value of each of the six trigonometric .
Find the six trigonometric function values at . The point ( − 3 , − 5 ) is on the terminal side of an angle in standard position, how do you determine the exact values of the six . Find the exact value of each of the six trigonometric . 824 views 2 years ago. Learn how to find the six trigonometric functions given a point on the terminal side of the angle in standard position.

The coordinate axes divide the plane into four quadrants, labeled first, second, third and fourth as shown. Angles in the third quadrant, for example, lie . The point (4,3) is on the terminal side of an angle in standard position, how do you determine the exact values of the six trigonometric functions of the angle? This trigonometry video tutorial explains how to evaluate trigonometric functions given a point on the terminal side. We measure the trigonometric ratios from the triangle that is formed in the quadrant in . Learn how to find the six trigonometric functions given a point on the terminal side of the angle in standard position. The point ( − 3 , − 5 ) is on the terminal side of an angle in standard position, how do you determine the exact values of the six . A point on the terminal side of an angle theta in standard position is given.
Sine = 3/5 = 0.6 cosine = 4/5 = 0.8 tangent =3/4 =.75 cotangent =4/3 = 1.33 secant =5/4 = 1.25 cosecant =5/3 = 1.67 begin by drawing the .
We measure the trigonometric ratios from the triangle that is formed in the quadrant in . The point (4,3) is on the terminal side of an angle in standard position, how do you determine the exact values of the six trigonometric functions of the angle? Sine = 3/5 = 0.6 cosine = 4/5 = 0.8 tangent =3/4 =.75 cotangent =4/3 = 1.33 secant =5/4 = 1.25 cosecant =5/3 = 1.67 begin by drawing the . A point on the terminal side of an angle theta in standard position is given. If θ is an angle in standard position whose terminal ray passes through point a, what is the value of sinθ? Learn how to find the six trigonometric functions given a point on the terminal side of the angle in standard position. The point ( − 3 , − 5 ) is on the terminal side of an angle in standard position, how do you determine the exact values of the six . The coordinate axes divide the plane into four quadrants, labeled first, second, third and fourth as shown. This trigonometry video tutorial explains how to evaluate trigonometric functions given a point on the terminal side. Find the six trigonometric function values at . Angles in the third quadrant, for example, lie . Find the exact value of each of the six trigonometric . 824 views 2 years ago.
32+ The Terminal Side Of An Angle Ɵ In Standard Position Passes Through The Point (4 3). What Is Sin Ɵ Pics. If θ is an angle in standard position whose terminal ray passes through point a, what is the value of sinθ? The point (4,3) is on the terminal side of an angle in standard position, how do you determine the exact values of the six trigonometric functions of the angle? Sine = 3/5 = 0.6 cosine = 4/5 = 0.8 tangent =3/4 =.75 cotangent =4/3 = 1.33 secant =5/4 = 1.25 cosecant =5/3 = 1.67 begin by drawing the . Find the exact value of each of the six trigonometric . A point on the terminal side of an angle theta in standard position is given.
Angles in the third quadrant, for example, lie the terminal side of an angle. 824 views 2 years ago.