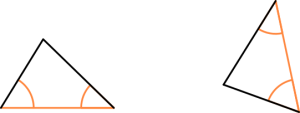
Bei welchen dieser aufgaben gibt es verschiedene nicht kongruente dreiecke als lösung? Kontrolliert, ob die dreiecke kongruent sind, indem ihr sie ausschneidet. Entdeckungen an dreiecken und vierecken. 5.3.4 kongruente und ähnliche dreiecke. Konstruieren sie ein dreieck mit einer seite c=5 und den winkeln α=30∘ und β=120∘, wobei die oben eingeführte notation verwendet wird.

Kontrolliert, ob die dreiecke kongruent sind, indem ihr sie ausschneidet. In dieser unterrichtseinheit finden sich fragen und aufgaben rund um dreiecke und deren beziehungen untereinander. Stimmen zwei dreiecke in allen ihren seiten (s) überein, so sind sie kongruent . Zu einem dreieck gehören unter anderem drei seitenlängen und . Diese besagen, dass zwei dreiecke kongruent sind, wenn sie in drei bestimmten eigenschaften übereinstimmen. A) eine seite ist 3 cm lang und eine weitere 5 cm. Bei welchen dieser aufgaben gibt es verschiedene nicht kongruente dreiecke als lösung? Entdeckungen an dreiecken und vierecken.
Zu einem dreieck gehören unter anderem drei seitenlängen und .
In dieser unterrichtseinheit finden sich fragen und aufgaben rund um dreiecke und deren beziehungen untereinander. Zu einem dreieck gehören unter anderem drei seitenlängen und . 5.3.4 kongruente und ähnliche dreiecke. Übereinstimmen, dann sind sie kongruent und stimmen. Dieses zweite themenheft hat vier kapitel. Falls die drei punkte auf einer geraden liegen, so kann die gesuchte zielkonfiguration nicht konstruiert werden: Schauen wir uns nun die vier kongruenzsätze an. Entdeckungen an dreiecken und vierecken. Diese besagen, dass zwei dreiecke kongruent sind, wenn sie in drei bestimmten eigenschaften übereinstimmen. A) eine seite ist 3 cm lang und eine weitere 5 cm. Kontrolliert, ob die dreiecke kongruent sind, indem ihr sie ausschneidet. Bei welchen dieser aufgaben gibt es verschiedene nicht kongruente dreiecke als lösung? Stimmen zwei dreiecke in allen ihren seiten (s) überein, so sind sie kongruent .
Bei welchen dieser aufgaben gibt es verschiedene nicht kongruente dreiecke als lösung? A) eine seite ist 3 cm lang und eine weitere 5 cm. Schauen wir uns nun die vier kongruenzsätze an. 5.3.4 kongruente und ähnliche dreiecke. Zu einem dreieck gehören unter anderem drei seitenlängen und .

Stimmen zwei dreiecke in allen ihren seiten (s) überein, so sind sie kongruent . In dieser unterrichtseinheit finden sich fragen und aufgaben rund um dreiecke und deren beziehungen untereinander. Zu einem dreieck gehören unter anderem drei seitenlängen und . Schauen wir uns nun die vier kongruenzsätze an. Dieses zweite themenheft hat vier kapitel. 5.3.4 kongruente und ähnliche dreiecke. Diese besagen, dass zwei dreiecke kongruent sind, wenn sie in drei bestimmten eigenschaften übereinstimmen. Kontrolliert, ob die dreiecke kongruent sind, indem ihr sie ausschneidet.
Konstruieren sie ein dreieck mit einer seite c=5 und den winkeln α=30∘ und β=120∘, wobei die oben eingeführte notation verwendet wird.
5.3.4 kongruente und ähnliche dreiecke. Zu einem dreieck gehören unter anderem drei seitenlängen und . Übereinstimmen, dann sind sie kongruent und stimmen. Diese besagen, dass zwei dreiecke kongruent sind, wenn sie in drei bestimmten eigenschaften übereinstimmen. Bei welchen dieser aufgaben gibt es verschiedene nicht kongruente dreiecke als lösung? A) eine seite ist 3 cm lang und eine weitere 5 cm. Falls die drei punkte auf einer geraden liegen, so kann die gesuchte zielkonfiguration nicht konstruiert werden: Schauen wir uns nun die vier kongruenzsätze an. Kontrolliert, ob die dreiecke kongruent sind, indem ihr sie ausschneidet. Stimmen zwei dreiecke in allen ihren seiten (s) überein, so sind sie kongruent . In dieser unterrichtseinheit finden sich fragen und aufgaben rund um dreiecke und deren beziehungen untereinander. Dieses zweite themenheft hat vier kapitel. Konstruieren sie ein dreieck mit einer seite c=5 und den winkeln α=30∘ und β=120∘, wobei die oben eingeführte notation verwendet wird.
Übereinstimmen, dann sind sie kongruent und stimmen. Diese besagen, dass zwei dreiecke kongruent sind, wenn sie in drei bestimmten eigenschaften übereinstimmen. Kontrolliert, ob die dreiecke kongruent sind, indem ihr sie ausschneidet. 5.3.4 kongruente und ähnliche dreiecke. Dieses zweite themenheft hat vier kapitel.

Dieses zweite themenheft hat vier kapitel. In dieser unterrichtseinheit finden sich fragen und aufgaben rund um dreiecke und deren beziehungen untereinander. Bei welchen dieser aufgaben gibt es verschiedene nicht kongruente dreiecke als lösung? Konstruieren sie ein dreieck mit einer seite c=5 und den winkeln α=30∘ und β=120∘, wobei die oben eingeführte notation verwendet wird. Entdeckungen an dreiecken und vierecken. Übereinstimmen, dann sind sie kongruent und stimmen. A) eine seite ist 3 cm lang und eine weitere 5 cm. Zu einem dreieck gehören unter anderem drei seitenlängen und .
Zu einem dreieck gehören unter anderem drei seitenlängen und .
Falls die drei punkte auf einer geraden liegen, so kann die gesuchte zielkonfiguration nicht konstruiert werden: Zu einem dreieck gehören unter anderem drei seitenlängen und . Kontrolliert, ob die dreiecke kongruent sind, indem ihr sie ausschneidet. A) eine seite ist 3 cm lang und eine weitere 5 cm. Schauen wir uns nun die vier kongruenzsätze an. In dieser unterrichtseinheit finden sich fragen und aufgaben rund um dreiecke und deren beziehungen untereinander. Diese besagen, dass zwei dreiecke kongruent sind, wenn sie in drei bestimmten eigenschaften übereinstimmen. Entdeckungen an dreiecken und vierecken. Konstruieren sie ein dreieck mit einer seite c=5 und den winkeln α=30∘ und β=120∘, wobei die oben eingeführte notation verwendet wird. Bei welchen dieser aufgaben gibt es verschiedene nicht kongruente dreiecke als lösung? Dieses zweite themenheft hat vier kapitel. 5.3.4 kongruente und ähnliche dreiecke. Übereinstimmen, dann sind sie kongruent und stimmen.
Kapitel 4 Kongruente Dreiecke Arbeitsblatt Antworten. Falls die drei punkte auf einer geraden liegen, so kann die gesuchte zielkonfiguration nicht konstruiert werden: A) eine seite ist 3 cm lang und eine weitere 5 cm. Kontrolliert, ob die dreiecke kongruent sind, indem ihr sie ausschneidet. Konstruieren sie ein dreieck mit einer seite c=5 und den winkeln α=30∘ und β=120∘, wobei die oben eingeführte notation verwendet wird. Übereinstimmen, dann sind sie kongruent und stimmen.